Case Study#11 인공지능에 관한 잡담 : 머신러닝 알고리즘의 원리와 인공지능

최근 가장 핫한 기술 분야 중 하나인 인공지능(AI, Artificial Intelligence)의 기원에 대해서는 여러 설이 있지만 개인적으로 가장 좋아하는 설명은 컴퓨터 알고리즘에서 변형, 발전되어 왔다는 주장이다. 영화 ‘이미테이션 게임’으로도 잘 알려진 앨런 튜링의 ‘튜링 테스트’에서 처음으로 ‘인공 지능’이라는 개념을 구분하는 개념이 제되어, 그 단어 역시 현대까지 이어져 사용되고 있다.

알고리즘이란, (대중적으로는) 고수준 컴퓨터 언어 코드를 통해 특정 기능을 수행할 수 있도록 하는 체계, 혹은 그러한 사고 흐름을 말한다. 그래서 알고리즘의 종류에는 A-Z까지 모든 경우의 수를 고려하는 Brute Force나, cache 등에 데이터를 저장/메모하여 재귀적/반복적으로 풀어나가는 DP등 수많은 종류가 존재한다. ‘어떤 일이 진행되는 과정이나 체계’라는 말이 ‘알고리즘’이라는 말과 자주 혼용되는 것도 이 때문일 것이다. 그러나, 이러한 구세대식 알고리즘은(그렇다고 그들이 구식이라는 의도는 아니다. 단순히 오래되었음을 이야기하고자 했다.) 지극히 개인적인 견해이지만, 복잡한 요소가 ‘관계성’을 띄며 혼재하는 ‘빅 데이터’를 다룰 때에는 지나치게 방대한 크기, 길이, 복잡도로 인해 그 개념이 우리 생활에 더 맞닿아 있을수록 비효율적인 방식이 되어갔다. 이를 개선하여준 것이 ‘인공지능’의 관점에서 만들어낸 새로운 알고리즘인 머신러닝/딥러닝 알고리즘이다.

이들의 일반적인 목적은 ‘어떤 값’에 ‘영향력이 있는’ 요소들의 데이터를 학습하여 차후 이 데이터만으로도 ‘어떤 값’을 예측해 내는것이다. 이때 값을 계산하여 예측하는 함수를 ‘가설 함수’라고 하고, 머신 러닝의 목적은 최적의 가설함수를 찾는 것이며, 딥러닝은 수많은 가설함수들끼리의 연결로 이루어진 은닉층들을 거쳐 마치 인간의 실제 뇌가 작동하는 방식을 모방하여(인공 신경망) 더욱 복잡하고 복합적인 연산을 해낸다는 차이점이 있다(매우 단편적인 비유이다...).

머신러닝의 전반적인 개념에 대해 설명하자면, 우선 크게 2가지의 방식이 있다. 이들이 도출하고자 하는 값이 이산적(Y/N 등)이라면 ‘분류 모델’, 연속적이라면 ‘회귀’ 모델을 사용한다. 개념상 회귀 모델이 더 일반적인 경우이므로 이를 위주로 먼저 적어보겠다.

‘회귀(Regression)’의 목적은 특정 값(데이터)을 넣었을 때 예측값을 도출하는 함수인 ‘가설함수(Hypothesis Function)’를 만드는 것이다. 가설함수는 수많은 데이터의 학습을 통해 생성되는데, 이때 사용하는 함수의 종류에 따라 선형회귀, 다항 회귀 등의 이름으로 불린다. 이들의 학습은 처음에는 랜덤한 함수로 초기화해서 시작하여, 가설함수의 함숫값인 ‘예측값’과 실제 데이터에 있는 ‘답(실제값)’의 차이를 최소화하는 방식으로 이루어진다. 더 정확히 말하자면 가설함수를 구성하는 계수, 상수를 ‘가중치(weight), 편향(bias)’이라고 하는데, 이들의 구성에 따라 자연히 가설함수의 함숫값도 바뀌게 된다. 즉 (함숫값)-(실제값)인 오차도 변하게 된다. 따라서 우리는 이 ‘오차’를 가중치와 편향에 대한 함수로 쓸 수 있게 된다. 이때 이 함수를 ‘손실함수(J Function)’라고 한다. ‘손실함수’는 오차를 계산하는 방식에 따라 ‘평균제곱오차’나 ‘로그오차’ 등 다양한 방식이 있지만, 일반적으로는 평균제곱오차(mean squared error, mse)를 사용한다.

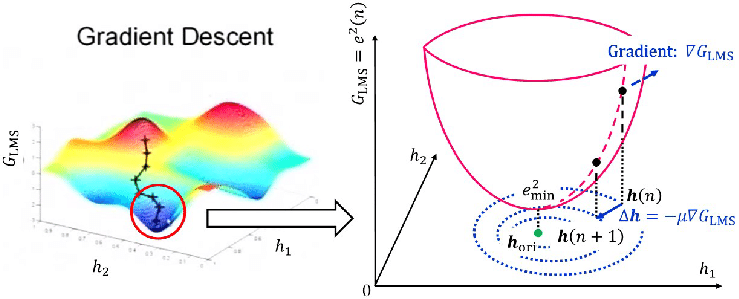
다시 가설함수의 학습 이야기로 돌아와서, 손실함수는 그 자체로서 가설함수가 얼마나 실제 현상과 동떨어져있는지를 의미한다. 따라서 손실함수가 최솟값일 때의 정의역값인 가중치와 편향을 찾는다면, 그것이 즉 최적의 가설함수를 완성하는 조건이 된다고 할 수 있다. 따라서 손실함수의 최솟값을 찾기 위해 우리는 손실함수 자체에 대한 분석을 실행한다. 손실함수를 가중치와 편향에 대하여 편미분하는 것이다. 그러면 손실함수의, 가중치와 편향에 대한 기울기/변화의 방향 값이 나온다. 즉, 현재 값에서 이 방향의 반대로 빼주면 (역방향으로 업데이트 해주면) 해당 방향으로 이동하며 함숫값이 더 작은 방향으로 이동하게 된다. 이를 충분히 많이 반복하여 최솟값에 가장 근사한 지점을 찾아내면 된다. 이 방식을 ‘경사 하강법(Gradient Descent)’이라고 한다. 단, 이 방식에는 한계점이 있는데, 만약 이 손실함수가 위 그림과 같이 단순히 아래로 볼록(보통 convex하다고 표현한다.)하지 않다면, 혹은 여러개의 극소값을 가진다면, 이 방식은 최적의 값을 찾지 못하는 경우가 생긴다는 것이다. (최초 지점을 어떻게 잡느냐에 따라 편차가 커질 수도 있게 된다.) 그러나 실험 결과 해당 극소값의 값을 사용하여도 충분히 유의미한 가설함수가 만들어졌고, 그렇지 않다고 하더라도 가설함수를 초기화할 때 여러 번 시도하여 나온 다양한 손실함수로 경사하강을 시행한 뒤 그 중의 최솟값을 선택하는 방법도 있다. 이 경우 충분히 경사하강법의 단점을 보완할 수 있게 된다. (Random Forest-스러운 방법)

그러나 이런 최적 가설함수를 찾아도 몇 가지 문제점이 여전히 존재한다. 그중 대표적인 것이 과적합 현상(over-fitting)이다. 얼핏보면 데이터에 대해 충분히 많이 학습을 하면 할수록 좋은 모델이 나올 것 같지만 실상은 그렇지 않다. 아래의 그래프처럼 학습의 횟수가 특정 임계점을 넘으면 가설함수가 해당 데이터’에만’ 최적화되고, 새로운 데이터로 예측을 시행하였을 때 오히려 정확도가 떨어지는 현상이 발생한다. 마치 어떤 사과 하나를 두고, ‘이것이 사과이다.’라고 학습을 하였는데, 다른 사과를 보여주었을 때 인식을 하지 못하는 것과 같다. 학습한 것에 대해 충실히 학습을 한 것은 맞지만, 사실 실제 세계에서 모든 사과가 100% 똑같이 생기지는 않았다. 따라서 위의 경우는 ‘사과’라는 개념 자체를 학습했다고 하기 보다는 ‘어느 특정 그 사과’만을 학습했다고 해야 할 것이다. 이 머신러닝 알고리즘에도 마찬가지로 그 데이터값’만’ 보다는 전체적인 개념, 그리고 그의 본질을 학습하기 위해 여러 방식을 사용한다.

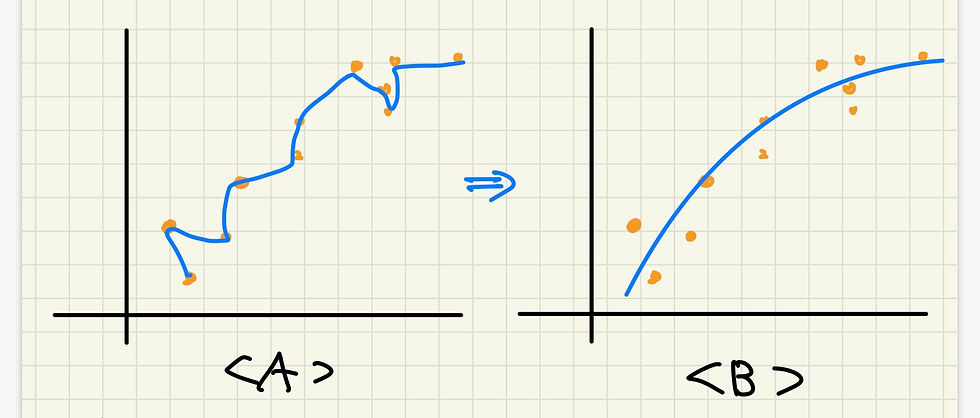
첫째로 가장 단순하게는 ‘early-stopping’을 통해 학습횟수를 조절한다. 둘째로 정규화(L1, L2)등의 방식을 통해 가중치와 편향 자체의 크기를 줄인다. 도식적으로 보았을 때 과적합 상황은 <A>의 상황과 비슷한 경우가 많다. 이를 <B>와 같은 그래프가 되도록 잘 조정해주는 것이다. (이에 대한 python 코드 구현은 다음 Github에서 확인할 수 있다. https://github.com/skykongkong8/Machine_Learning_Practice)

지금까지 머신러닝 알고리즘의 (그것도 회귀방식에 대한) 원리에 대해 알아보았다. 이 원리만 잘 파악하고 있다면 딥러닝 알고리즘 역시 이와 기본적인 궤를 같이하기 때문에 받아들이는 것 자체에서는 큰 문제가 없다. 아주 짧게만 적어보자면 이러한 기법을 더 다양한 연결관계를 가지고 계산(인공 신경망 구조와 deep 은닉층..)하여 더 복합적인 의미를 가지고 있는 결과값을 내는 것이다. 이에 대해서는 다음에 더 자세히 적어보겠다.

이러한 인공지능의 작동 방식을 보고 개인적으로 가장 매력적이라고 생각했던 점은 바로 여러 요소들을 ‘한꺼번에’ 고려하는 것을 코드로 구현해냈다는 점이다. 보통의 인간은 어떤 데이턴 통계를 보고도, 고도의 숙련된 전문가가 아닌 이상 그의 의미나 예측값들을 객관적으로 도출해내기 솔직히 매우 어렵다. 크고 작은 고유의 생각의 편향이나, 버릇, 혹은 예기치 못한 실수와 같은 여러 돌발적인 상황이 발생하기 십상이기 때문이다. 그러나 알고리즘은 다르다. 인간과는 비교도 안되게 빠른 속도로 학습하며, 학습 데이터 자체에 조작이 있지 않은 이상 주관이라는 개념이 존재할 수 없다. 이가 시사하는 바는 매우 크다고 생각한다. 단순히 데이터에 대한 결과도출 뿐 아니라, ‘선택’이라는 것이 존재하는 모든 영역의 ‘가장 객관적인 답’을 도출해낼 수 있다는 의미까지 확장될 수 있기 때문이다.

어떤 쟁점사항에 대한 결정을 내릴 때, 인간은 본성적으로 좋다/나쁘다 등의 이분법적 가치판단을 자신이 인지하지도 못하는 사이에 내린다고 한다. ([책] - 팩트풀니스 참조) 그러나 우리 인생의 대부분이 이러한 선택의 순간들의 연속인데 반해 실제 세상은 그렇게 단순한 A or B 구조로만 이루어져 있지 않은 경우가 훨씬 많다. 선택을 하여도 예상치 못한 결과가 나오는 경우가 오히려 대다수이며 당장은 맞은 것 같더라도 분명 다른 관점에서 보면 미처 몰랐던 일들이 알게 모르게 존재한다. 이렇듯 망망대해를 표류하는 것과 같은 우리네의 인생에서, 인공지능은 여러 요소를 “한꺼번에 고려”하게 해주는 좋은 도구가 되어줄 것이라고 생각한다.

예를 들어, 기계공학을 공부하던 중 한 장치를 설계하면서 겪었던 일이 있었다. 해당 장치는 관에 기체 유동을 받아서 중간에 기체 흐름의 속도를 변화시켜 압력을 발생시키는 장치(Venturi 관)이었는데, 이를 위해서 기체가 들어가는 곳에서의 마찰/turbulance로 인한 손실을 최소화하려면 관의 길이를 늘려야 했고(각도가 서서히 상승해야 했으므로), 전반적인 재료의 가격이나 현실성을 따지면 마냥 늘일수는 없는 상황이었다. 이러한 경우를 담당 교수님께서는 Engineer’s Decision이 오는 순간이라고 하셨는데, 이런 경우 적당한 기준점을 찾는 데에 머신러닝과 같은 알고리즘이 좋은 방향을 추천해줄 수 있을 것이라는 생각이 들었다. 이외에도 머신러닝은 넷플릭스, 유튜브의 추천 시스템과 같은 다양한 분야를 어우르는 범주에서 ‘선택’이 필요한 순간마다 활용되고 있다.

그러나 이렇게 뛰어난 인공지능의 기능성에도 불구하고, 인공지능이 인간의 역할을 완전히 대신할 수 있는 것은 아니다. 인공지능은 ‘계산’이나 ‘학습’ 등과 같은 특정 영역에 있어 인간보다 우위에 있을 뿐이다. 다소 극단적일 수 있지만 이는 마치 나무를 자르기 위한 톱이 인간의 맨손보다 무언가를 자르는 데 있어 더 효과적일 뿐이고, 톱 자체가 인간을 대신할 수 없는 것과 같다. (위와 같은 사고방식 역시 부분적인 측면의 우수성만 보고 전체적인 우열을 가리려는 이분법적 사고 방식의 일종이라는 생각이 든다.) 인공지능은 인간이 만들어낸 ‘조금 더 신기한 도구’일 뿐이라고 생각한다. 물론 유사성이 짙은 나머지 ‘대상화’나 기능이 너무 뛰어난 나머지 아직 정립이 잘 되지 않은 ‘사용 윤리’와 같은 쟁점사항들이 남아있지만, 이는 시간이 해결해 줄 문제라고 생각한다(지금껏 대부분의 기술 발전의 역사를 보면 늘 그러했다).

딥 러닝과 머신러닝에 관련된 좀 더 구체적인 Python 코드 구현은 아래 깃허브 주소에서 확인할 수 있다.

https://github.com/skykongkong8

앞으로 이와 같이 꼭 인공지능이 아니더라도 다양한 문제에 관한 생각들을 별 형식 없이 적어볼 생각이다. 개인적인 견해이고, 아직 부족한 공부에서 비롯된 생각들이다 보니 부정확하거나 편향 되어있는 글일 수 있음을 감안해주기를 바란다.